Finding Maneuvering Speed At Light Weights

A common FAA knowledge test question goes like, “Which of these speeds is not found on the airspeed indicator?” The answer is usually design maneuvering speed, also known as V_A. Many students might then wonder why it is not found on the airspeed indicator along with other important V speeds such as V_NE and V_FE. Perhaps it is really not that important? Well, the FAA certainly believes that it is important enough to warrant a test question!

One of the reasons V_A isn’t found on the airspeed indicator is because, like V_X and V_Y, maneuvering speed changes with weight. The speed found in the POH or placard is applicable for a particular weight, usually maximum gross. We often do not fly our airplanes at maximum gross takeoff weight, so what happens to maneuvering speed as we fly at these lighter weights? It decreases! Let me offer a simple and thorough explanation as to why that is, as well as provide ways to calculate a “new” maneuvering speed if flying below maximum gross weight.

THE SIMPLE EXPLANATION

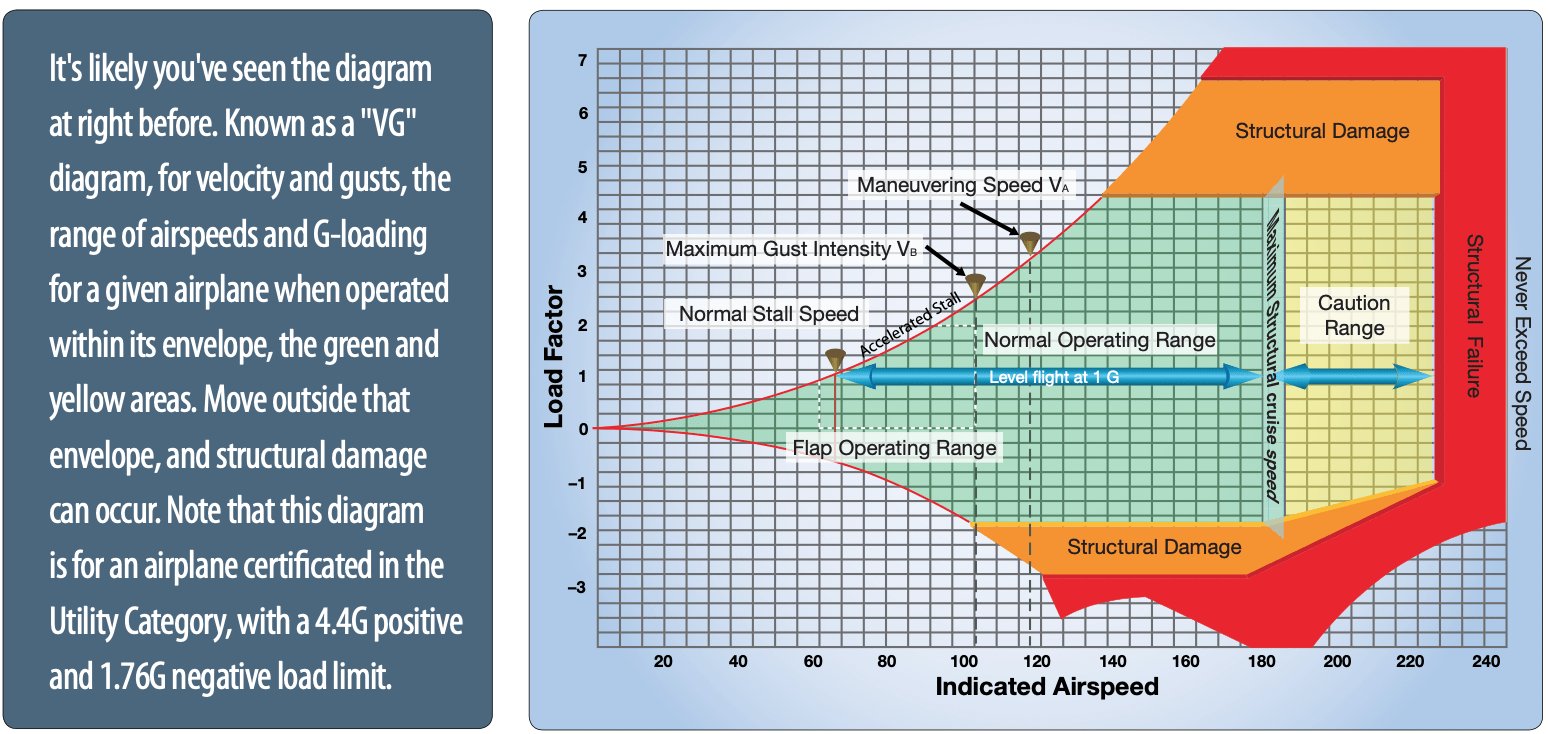
Unless the airplane is maneuvering, we really only worry about V_A in turbulence. That’s because turbulence often results in vertical gusts that momentarily increase or decrease the angle of attack an airplane’s wing is flying at. There exists a direct relationship between the amount of lift produced and the angle of attack, so if angle of attack is doubled, then the amount of lift produced is also doubled. Normally, the amount of lift produced by an airplane is equal to weight; we call this 1G loading. In this case, “G” really just describes the ratio of lift to weight. If the angle of attack is doubled, thereby doubling lift, the ratio of lift to weight is now 2:1—we call this 2G loading. Airplanes are certified to structurally handle a certain amount of G—this is called the “limit-load factor” and is 3.8G for normal category airplanes, 4.4G for the utility category and 6G for aerobatic airplanes. Flying at or below the airplane’s weight-adjusted maneuvering speed helps us ensure that we never meet or exceed the limit-load factor.

How does this work? For every cruising airspeed, the airplane is flying at a particular angle of attack. During cruise, the airplane is flying at a relatively low angle of attack. During slow flight, the airplane is flying at a higher angle of attack. From our primary flight training, we know that the airplane will stall if it exceeds the “critical angle of attack,” which happens to be about 18 degrees or so.

Let’s say the airplane is cruising at a speed that has it flying at nine degrees angle of attack. Because the airplane stalls at around 18 degrees angle of attack, the angle of attack can at most be doubled before the stall. In other words, the airplane will stall at 2G, which is less than 3.8G. Now, if that same airplane was instead cruising at a speed that has it flying at two degrees of angle of attack, the angle of attack can be increased nine-fold before stall. That means the stall will occur at 9G! This is much more than what the airplane is structurally certified for.

Because a stall will limit the G experienced, we would rather have the airplane stall momentarily than experience lasting structural damage. If we fly above maneuvering speed, the airplane can aerodynamically support the G, but cannot structurally support any G greater than the limit-load factor. If we fly below maneuvering speed, the airplane can structurally support more G, but cannot aerodynamically support more G, since the stall occurs at a G loading below limit-load factor. The maneuvering speed is the boundary between these two categories—it is the exact speed where the airplane will stall at the limit-load factor.

THINGS GET WEIGHTY

So how does weight play a role? If the airplane is lighter, it needs to produce less lift to counteract weight, which means that the angle of attack for any given cruise speed will be lower than what it was before. Previously, the cruise speed may have put the airplane at six degrees angle of attack, which means that it would have stalled at 3G. But now, that same cruise speed may put the airplane at only 4.5 degrees angle of attack, which means that it will experience 4G before stalling! Flying at this cruise speed is now unacceptable considering that the limit-load factor is 3.8G. For this new weight, we must now fly at a different speed, one that results in a higher angle of attack. This will ensure that the airplane will stall before exceeding the limit-load factor. To increase the angle of attack that an airplane cruises at, speed must be decreased (think again about cruise vs. slow flight). Thus, when weight is reduced, maneuvering speed is also reduced.

SOME (SIMPLE?) MATH

How much should maneuvering speed be reduced for a given decrease in weight? There is a formula to calculate it! All we need is maneuvering speed at a given weight, along with the new weight. Divide the new weight by the published weight, take the square root and multiply by the published maneuvering speed. The math for this is presented in the formula above. There is also a rule of thumb if you find square roots inconvenient or scary. Take the percent decrease in weight and decrease maneuvering speed by half of that difference.

Which is better? It is important to note that the rule of thumb will always result in a slightly higher value for maneuvering speed than the formula at typical weights. This means that flying at the speed given by the rule of thumb may result in exceeding limit-load factor before stall. However, the difference between what the rule of thumb yields and what the formula yields is about one knot—insignificant for practical purposes. So, it’s hard to go wrong with using either.

The math for all this involves some calculus. Rather than reproduce it here, visit the online version of this article at: flyklvk.aero/maneuvering-speed/.

PLOTTING THE DIFFERENCE

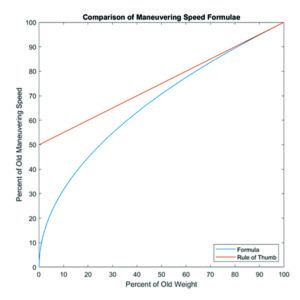
How good is the rule of thumb, and is it okay to use? As mentioned before, the rule of thumb is only a good approximation at weights close to gross weight. This is clear when we plot the two relations, as shown in the graph at bottom left, where the two curves predict essentially the same maneuvering speed toward the right end.

To highlight an egregious error: If weight is 0 percent—in other words, a 100-percent decrease in weight—then maneuvering speed should be 0. However, the rule of thumb says that maneuvering speed should be decreased by only 50 percent (half of the 100-percent decrease in weight)!

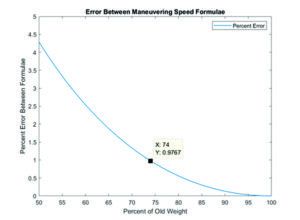
This is an exaggerated example, however, because empty weight constitutes a large part of the total weight. Let’s look at a real-world case: a 1979 Piper Warrior II. This airplane has a maximum gross weight of 2325 lbs. Empty weight is 1500 lbs., which is already almost 65 percent of the maximum allowed weight. After adding a 150-lb. pilot and a quarter tank of fuel, the realistic minimum weight at which this airplane should be flying is around 1725 lbs. This is 74 percent of its gross weight. Looking at the graph at bottom right, the percent difference in predicted maneuvering speeds when loaded to 74 percent of gross weight is 0.98 percent. For this airplane, where maneuvering speed at gross weight is 111 knots, the rule of thumb yields a result one knot higher than the actual formula—a relatively insignificant error. Also, this is the worst possible error, because the error decreases as weight is increased.

So, we can conclude that the rule of thumb is good for practical purposes.

Srinath Nandakumar is an aeronautical and avionics engineer, and an Iowa-based flight instructor.