Pilots depend on their training and memory to get through many tasks. But no one can remember everything there is to know about flying, especially its more arcane aspects. Thus, the memory gouge was invented, to help us remember what we’re supposed to do and when.
A gouge really is nothing more than a clever saying—east is least, west is best—or a rule intended to remind us of something we already know. One thing about memory gouges is there’s virtually no end to them. Another thing, ironically, is we tend to forget them. With that in mind, here’s a quick refresher on a gouge designed to help us fly a glideslope.
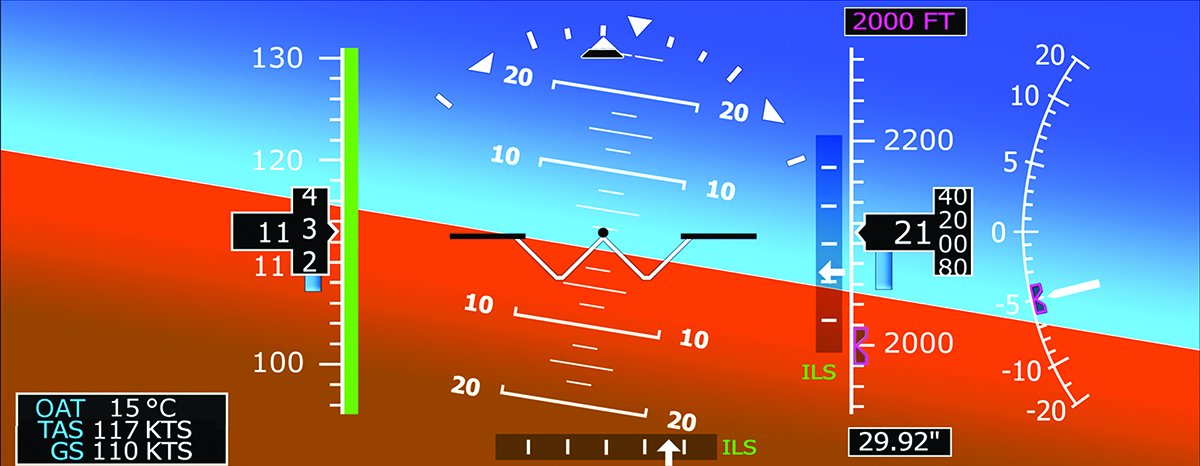
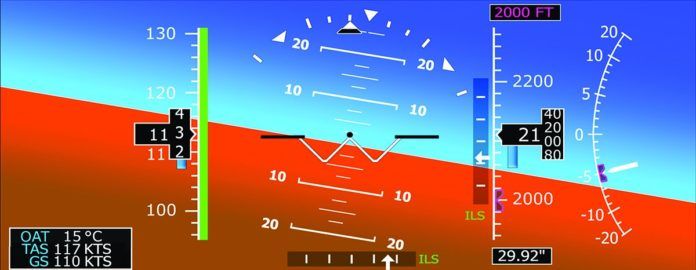
Rule Of Three
The Rule of Three got both its name and its reason for existence from the standard three-degree glideslope of an ILS approach. These days, you can expect the same descent angle from an ILS, LPV or LNAV/VNAV approach, i.e., those procedures with a decision height or altitude. Although exceptions abound, three degrees long ago was settled upon as the preferred angle of descent to a runway when executing an ILS. The three-degree glideslope affords us a relatively flat descent, helping ensure we can maintain control and fly a properly configured airplane at an appropriate airspeed without accelerating. That’s one of the fundamentals of establishing a stable approach.
A three-degree glideslope also simplifies some basic things for the instrument pilot. One of them is that a three-degree descent uses up 318 feet of altitude for each nautical mile traveled. But 318 is a messy number—it’s not easy to multiply in your head. Since we’re aiming for a rule of thumb here, we can round it down slightly to 300 feet per nm to make it much more manageable. So, if the final approach fix is six miles from the runway threshold, we’ll want to cross it 2000 feet above the threshold’s elevation to intercept the glideslope and begin descending.
Establish your standard approach configuration—landing gear and approach flaps, if any, plus power setting and nose-down pitch angle. Congratulations: You just established a stable approach. (The airplane’s pitch angle may or may not be three degrees down, depending.) Small corrections may be necessary for wind, but you’re already in the ballpark.
False Glideslope?
The Rule of Three also can help us on an ILS by ensuring we’re flying the correct glideslope. False glideslopes—usually at much steeper angles than three degrees—can be generated by an ILS and if we get a late vector or delay our descent, it’s possible to intercept one and try to follow it. Nine degrees is a commonly cited descent angle for a false glideslope, and following it is not a good idea. Executing the missed approach might be a good idea.
The Rule of Three affords us an easy and quick check to ensure we’re on the correct, three-degree glideslope: Using the example we just gave, if the three-degree glideslope we’re intercepting is approximately 2000 feet above the field elevation while we’re approximately six miles from the threshold, we’re good to go. Five miles? Call it 1700 feet, and 1200 at four nm. All of which is another argument in favor of intercepting a glideslope in level flight from below, instead of descending to it.
Other Uses
The Rule of Three can come in handy elsewhere on the ILS. For example, presume you’re 600 feet above the threshold elevation on an approach. How far are you from the threshold? Divide the agl altitude in feet (600) by three and drop the zeros. The result is two, which approximates your distance from the threshold in nautical miles.
Because the math works both ways, we also can use the Rule of Three to help determine what our altitude on the ILS should be if we know the distance to the threshold. For example, if we’re three miles from the runway, we should be about 900 feet above the threshold. Both calculations also can help us decide when to begin descending for a runway when executing a visual approach and we want to use a stable, three-degree descent angle as on an ILS.
Not Three
While we’re talking about gouges to use on the ILS, what descent rate do we need to maintain the three-degree glideslope? It depends on groundspeed, of course, but it’s easy to ballpark: Just multiply your groundspeed by five. If groundspeed is 120, 120 * 5 = 600. Use a 600-fpm descent and, again, you’ll be in the ballpark. Another way to get the same number is to add a zero to your groundspeed, then divide by two. Thus, our same 120-knot groundspeed becomes 1200, divided by two produces 600 again.
With modern avionics, we sometimes get caught up in trying to get the answer to a question from the box and forget to fly the plane. Using gouges like the Rule of Three can simplify everything.
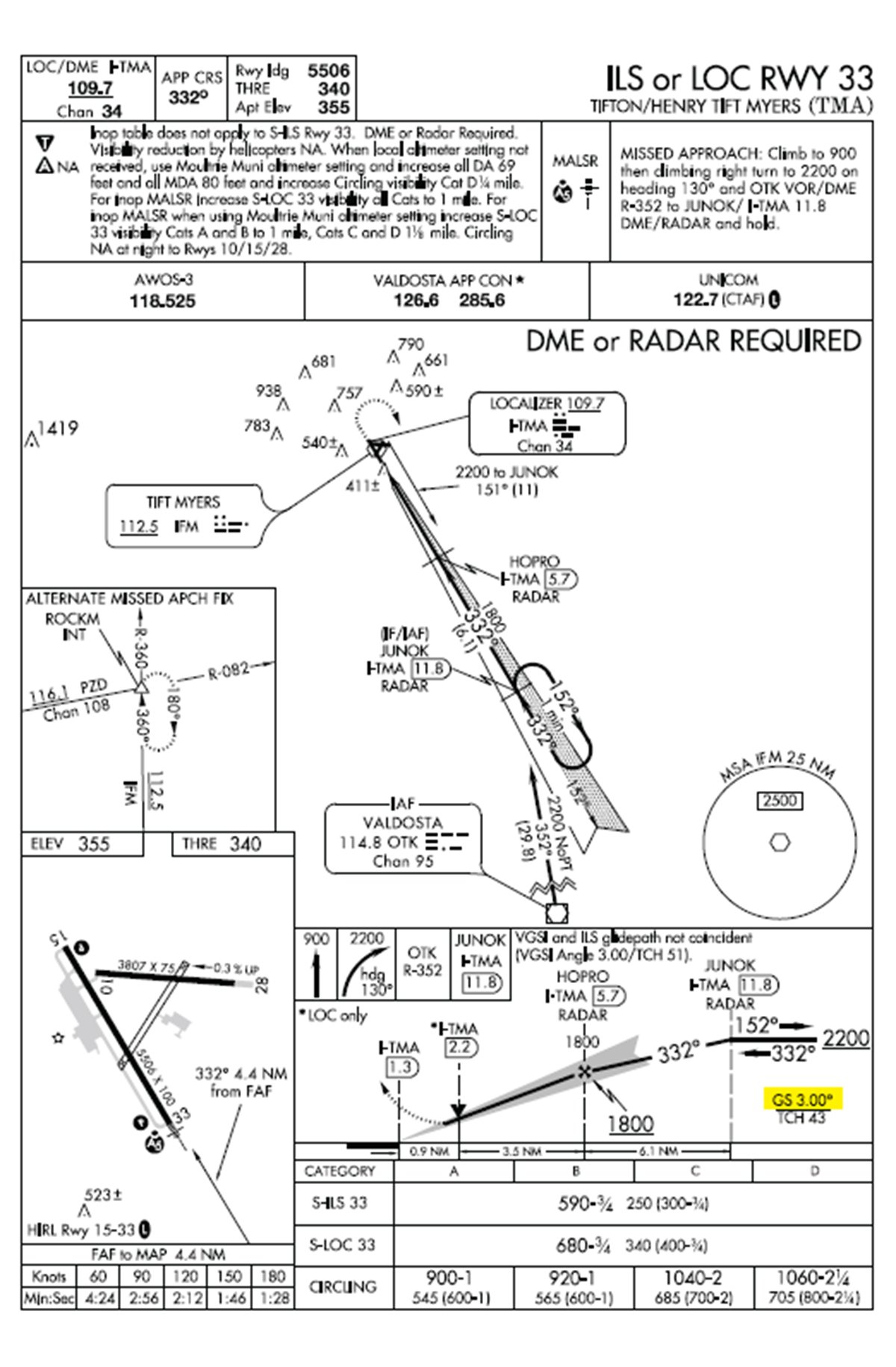
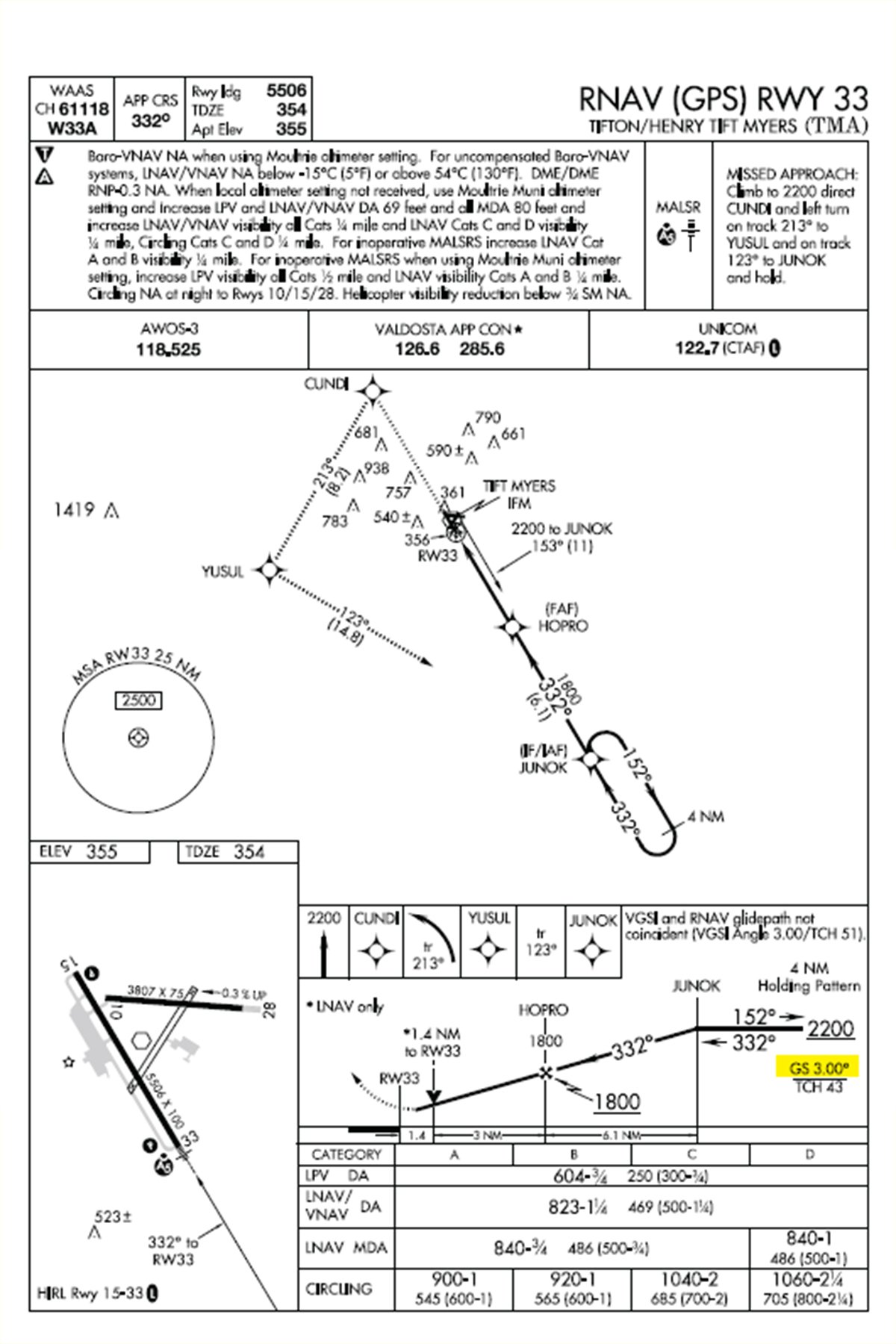
Because the Rule of Three is based on geometry and not approach procedure design, the same rules of thumb described in the article’s main text and applying to a standard ILS also work when considering an LPV or LNAV/VNAV approach. Consider the two procedures described on the plates reproduced at right for Runway 33 at the Henry Tift Myers Airport (KTMA) in Georgia.
As highlighted in yellow, both feature a three-degree glideslope. Both even use the same final approach fix and crossing height. Although both approaches allow a descent to 250 feet agl, the published decision height/decision altitude are not the same, thanks to different criteria applying to ILS and RNAV (GPS) procedures.